bonawerx.blogg.se - Insertion sort vs selection sort vs bubble sort

Insertion sort vs selection sort vs bubble sort code#

Some of the items I wanted to ensure was:

I ensured that they all have the same set of procedures during their run. I have now put together all of them in a single project on GitHub. Hence I started working on a simple implementation for each one of them.

Insertion sort vs selection sort vs bubble sort code#

Program: Write a program to implement insertion sort in C language.I had written about sorting algorithms (Tag: Sorting) with details about what to look out for along with their code snippets but I wanted a do a quick comparison of all the algos together to see how do they perform when the same set of input is provided to them. Now, let's see the programs of insertion sort in different programming languages. It is because, in insertion sort, an extra variable is required for swapping.

The space complexity of insertion sort is O(1).

The worst-case time complexity of insertion sort is O(n 2). That means suppose you have to sort the array elements in ascending order, but its elements are in descending order.

Worst Case Complexity - It occurs when the array elements are required to be sorted in reverse order.

The average case time complexity of insertion sort is O(n 2).

Average Case Complexity - It occurs when the array elements are in jumbled order that is not properly ascending and not properly descending.

The best-case time complexity of insertion sort is O(n).

Best Case Complexity - It occurs when there is no sorting required, i.e.

We will also see the space complexity of insertion sort. Now, let's see the time complexity of insertion sort in best case, average case, and in worst case. Move to the next elements that are 32 and 17. Now, the sorted array includes 8, 12, 25 and 31.

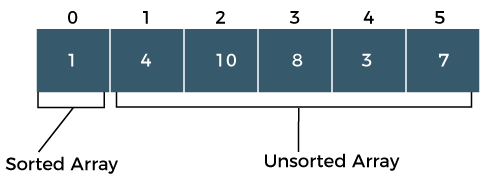
Move to the next items that are 31 and 32. Now, the sorted array has three items that are 8, 12 and 25. So, swap them.Īfter swapping, elements 25 and 8 are unsorted. Move forward to the next elements that are 31 and 8.īoth 31 and 8 are not sorted. Now, two elements in the sorted array are 12 and 25. Hence, the sorted array remains sorted after swapping. Along with swapping, insertion sort will also check it with all elements in the sorted array.įor now, the sorted array has only one element, i.e. Now, move to the next two elements and compare them. So, for now, 12 is stored in a sorted sub-array. That means both elements are already in ascending order. Initially, the first two elements are compared in insertion sort. It will be easier to understand the insertion sort via an example. To understand the working of the insertion sort algorithm, let's take an unsorted array. Now, let's see the working of the insertion sort Algorithm. Step 6 - Repeat until the array is sorted. Else, shift greater elements in the array towards the right. Step 4 - If the element in the sorted array is smaller than the current element, then move to the next element. Step3 - Now, compare the key with all elements in the sorted array. Step2 - Pick the next element, and store it separately in a key. Step 1 - If the element is the first element, assume that it is already sorted. The simple steps of achieving the insertion sort are listed as follows. Now, let's see the algorithm of insertion sort.

Adaptive, i.e., it is appropriate for data sets that are already substantially sorted.

Insertion sort has various advantages such as. Insertion sort is less efficient than the other sorting algorithms like heap sort, quick sort, merge sort, etc. Although it is simple to use, it is not appropriate for large data sets as the time complexity of insertion sort in the average case and worst case is O(n 2), where n is the number of items. The idea behind the insertion sort is that first take one element, iterate it through the sorted array. The same approach is applied in insertion sort. Similarly, all unsorted cards are taken and put in their exact place. If the selected unsorted card is greater than the first card, it will be placed at the right side otherwise, it will be placed at the left side. It is assumed that the first card is already sorted in the card game, and then we select an unsorted card. Insertion sort works similar to the sorting of playing cards in hands.

So, it is important to discuss the topic. This article will be very helpful and interesting to students as they might face insertion sort as a question in their examinations. The working procedure of insertion sort is also simple. In this article, we will discuss the Insertion sort Algorithm.